Programming: Arduino
Check out my other articles:
- Galaga: Failed Attempt at writing a Game
- Sudoku
- Blockade / Snake
- Farkle
- Minesweeper
- Blackjack
- ADC Graph
- Analogue Clock
- Tetris
Tetris
Tetris (Russian: Те́трис, pronounced [ˈtɛtrʲɪs]) is a tile-matching puzzle video game, originally designed and programmed by Russian game designer Alexey Pajitnov. It was released on June 6, 1984, while he was working for the Dorodnitsyn Computing Centre of the Academy of Science of the USSR in Moscow. He derived its name from the Greek numerical prefix tetra- (all of the game's pieces contain four segments) and tennis, Pajitnov's favorite sport.

|
Alexey worked as an artificial intelligence researcher at the Soviet Academy of Sciences at their Computer Center in Moscow. Tasked with testing the capabilities of new hardware, he would do so by writing simple games for them. He initially considered creating a game around pentominoes, which featured in puzzle games that he had enjoyed as a child, but felt that it might have been too complicated with twelve different shape variations, so the concept switched to tetrominoes, of which there are only seven variants. The Electronika 60 on which he was working had only a text-based display, so the tetrominoes were formed of letter characters. Realizing that completed lines resulted in the screen filling up quickly, Pajitnov decided to delete them, creating a key part of Tetris gameplay.
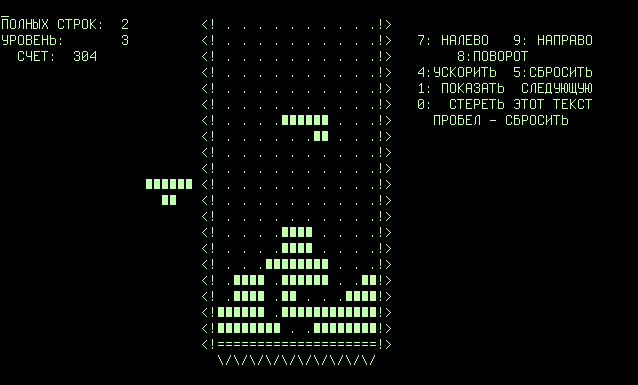
Who hasn't played Tetris? Its been a staple game on every mobile since the mid '90s Nokias. I just had to program a version for the Arduino ..
- Overview
- Game Play
- Code Fragments
- Rendering the Board
- Checking whether a Piece Movement is Valid
- Checking whether a Piece Rotation is Valid
- Updating the Board
- Wiring Diagram
- Downloads
Overview
"Tetrominos" are game pieces shaped like tetrominoes, geometric shapes composed of four square blocks each. A random sequence of tetrominos fall down the playing field (a rectangular vertical shaft, called the "well" or "matrix"). The objective of the game is to manipulate these tetrominos, by moving each one sideways (if the player feels the need) and rotating it by 90 degree units, with the aim of creating a horizontal line of ten units without gaps. When such a line is created, it disappears, and any block above the deleted line will fall. When a certain number of lines are cleared, the game enters a new level. As the game progresses, each level causes the tetrominos to fall faster, and the game ends when the stack of tetrominos reaches the top of the playing field and no new tetrominos are able to enter. Some games also end after a finite number of levels or lines.
Tetris suits itself well to the Arduino and SmartGPU2 screen - the graphics are not intensive and can easily be handled with this hardware. I elected to use a joystick (as it shares hardware with other games I have programmed) but the code could easily be modified to use four input buttons - left, right, drop and rotate.
Game Play
The four images below shows the game in action. After an initial splash screen, the user proceeds to the main game which is a conventional 20 high x 10 wide matrix. The right hand side of the screen shows the current level and rows completed. When the target number of rows is completed, the level increases as does the number of rows and the falling speed of the tetrominos.
Although there is no limit to the levels, the increase in speed would make levels above, say, 20 nearly impossible to complete. But hey, you can try!
 |
 |
|


|
 |
Code Fragments
The following code highlights areas of interest in the application. It is not intended to be a tutorial or a complete solution. I have provided the complete code for download and you may use or modify it as required.
The seven tetromino shapes are detailed below in their various allowable rotations. Refer to this when reviewing the code to makes sense of what each section is doing.


Rendering the Board
The board state is maintained in a single, two-dimensional array which is the 'regulation' ten elements wide and twenty elements high. The board is initialised with the default value '0' which indicates that the square is empty. As the board fills up, the array's elements are assigned a value between one and seven which correspond to the seven tetrominos - as defined in the constants section.
001 002 003 004 005 006 007 008 009 010 011 012 |
#define SHAPE_SQ_RED 1
#define SHAPE_T_YELLOW 2
#define SHAPE_Z_GREEN 3
#define SHAPE_Z_BLUE 4
#define SHAPE_L_PURPLE 5
#define SHAPE_L_BLUE 6
#define SHAPE_I_ORANGE 7
#define BOARD_X_MAX 10
#define BOARD_Y_MAX 20
byte board[BOARD_X_MAX][BOARD_Y_MAX] = {0};
|
Rendering of a single square is handled by the routine drawSquare() which accepts three parameters that represent the X and Y coordinates of the element to be rendered and the colour code. If the colour provided is not the background colour, the routine draws a single square in the nominated color on the screen. These X and Y values correspond to the element of the array being rendered and they are converted into screen coordinates using some predefined constants. It then draws a second square in black as an outline only to provide a border. If the nominated colour is the background colour (ie. the cell is empty) the routine draws a single, solid square in the background colour.
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 |
void drawSquare(byte x, byte y, int colour) {
if (colour != BACKCOLOUR) {
lcd.drawRectangle(BOARD_POS_X + (x * CELL_SIZE) + 1,
BOARD_POS_Y + (y * CELL_SIZE) + 1,
BOARD_POS_X + (x * CELL_SIZE) + (CELL_SIZE - 1),
BOARD_POS_Y + (y * CELL_SIZE) + (CELL_SIZE - 1),
colour, solidFill);
lcd.drawRectangle(BOARD_POS_X + (x * CELL_SIZE),
BOARD_POS_Y + (y * CELL_SIZE),
BOARD_POS_X + ((x + 1) * CELL_SIZE),
BOARD_POS_Y + ((y + 1) * CELL_SIZE),
BLACK, hollowFill);
}
else {
lcd.drawRectangle(BOARD_POS_X + (x * CELL_SIZE),
BOARD_POS_Y + (y * CELL_SIZE),
BOARD_POS_X + ((x + 1) * CELL_SIZE),
BOARD_POS_Y + ((y + 1) * CELL_SIZE),
BACKCOLOUR, solidFill);
}
}
|
Rendering the board is handled by a single routine named drawBoard(). It has a parameter that determines whether it should redraw the entire board including blank cells or not. There is no need to render the entire board if we are updating the board as the result of the final placement of a single tetromino.
If we are rendering blanks, line 004 - 010 simply clears the board to the background colour. It then iterates through all of the cells in the array and draws the square if it is not zero - ie. it has a non-zero valuing indicating it is part of a coloured block.
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 |
void drawBoard(boolean renderBlanks) {
if (renderBlanks) {
lcd.drawRectangle(BOARD_POS_X,
BOARD_POS_Y,
BOARD_POS_X + (BOARD_X_MAX * CELL_SIZE),
BOARD_POS_Y + (BOARD_Y_MAX * CELL_SIZE),
BACKGOLOUR,
solidFill);
}
for (int y = 0; y < BOARD_Y_MAX; y++) {
for (int x = 0; x < BOARD_X_MAX; x++) {
if (board[x][y] > 0) {
drawSquare(x, y, getColourCode(board[x][y]));
}
}
}
}
|
Checking whether a Piece Movement is Valid
Pieces in Tetris can be moved sideways and rotated as the pieces fall. Before allowing these movements, a test needs to be performed to see if the board positions / array elements that the part would occupy are actually empty. This test is performed by the canOccupySpace(byte type, byte rotation, int x, int y) method which accepts a piece type, and the new rotation and placement to test.
Control is handled by an outer switch (line 003) which is conditioned on the type parameter. For each tetromino type, an inner switch conditioned on the rotation is used to determine which array elements to test. As the red square is symmetrical both laterally and longitudinally, their is no inner switch (lines 005 - 013). The yellow 'T' tetromino is not symmetrical either laterally and longitudinally and hence has a rotation switch with all four cases defined (lines 017 - 053). The green 'Z' tetromino updates the same elements in the array whether when it is facing upwards or downwards - likewise when it is facing left or right.
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081 082 083 084 085 086 087 088 |
bool canOccupySpace(byte type, byte rotation, int x, int y) {
switch (type) {
case SHAPE_SQ_RED:
return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) &&
board[x][y] == 0 &&
board[x+1][y] == 0 &&
board[x][y+1] == 0 &&
board[x+1][y+1] == 0);
case SHAPE_T_YELLOW:
switch (rotation) {
case UP: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) &&
board[x-1][y] == 0 &&
board[x][y] == 0 &&
board[x+1][y] == 0 &&
board[x][y+1] == 0);
case LEFT: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) && (
y < 0 ? true : board[x][y-1] == 0) &&
board[x-1][y] == 0 &&
board[x][y] == 0 &&
board[x][y+1] == 0);
case DOWN: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX) &&
(y < 0 ? true : board[x][y-1] == 0) &&
board[x-1][y] == 0 &&
board[x][y] == 0 &&
board[x+1][y] == 0);
case RIGHT: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) &&
(y < 0 ? true : board[x][y-1] == 0) &&
board[x][y] == 0 &&
board[x+1][y] == 0 &&
board[x][y+1] == 0);
}
return false;
case SHAPE_Z_GREEN:
switch (rotation) {
case UP:
case DOWN: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) &&
board[x-1][y] == 0 &&
board[x][y] == 0 &&
board[x+1][y] == 0 &&
board[x+1][y+1] == 0);
case LEFT:
case RIGHT: return (x >= leftMostPos(type, rotation) &&
x <= rightMostPos(type, rotation) &&
y < (BOARD_Y_MAX - 1) &&
(y < 0 ? true : board[x+1][y-1] == 0) &&
board[x][y] == 0 &&
board[x+1][y] == 0 &&
board[x][y+1] == 0);
}
return false;
case SHAPE_Z_BLUE: ...
case SHAPE_L_PURPLE: ...
case SHAPE_L_BLUE: ...
case SHAPE_I_ORANGE: ...
}
}
|
The canOccupySpace() method is utilized by three helper methods which test whether the specified tetromino can move left, right or down by simply adjusting the current X and Y coordinates.+
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 |
bool canMoveDown(byte type, byte rotation, int x, int y) {
return canOccupySpace(type, rotation, x, y + 1);
}
bool canMoveLeft(byte type, byte rotation, int x, int y) {
return canOccupySpace(type, rotation, x - 1, y);
}
bool canMoveRight(byte type, byte rotation, int x, int y) {
return canOccupySpace(type, rotation, x + 1, y);
}
|
Checking whether a Piece Rotation is Valid
Rotating a piece requires a little more calculation. With the exception of the square, the footprint of each tetrominos change as it is rotated. Imagine the 'T' shaped tetromino shown below travelling down the left most side of the board ..
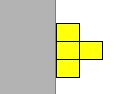
.. is rotated around it's central piece. The piece cannot rotate properly but if there is enough space to the right, the piece will be pushed over to allow it to rotate correctly. This happens the same way when the piece is travelling down the right hand side of the board however tetrominos are not pushed aside if the rotation is blocked by another piece.
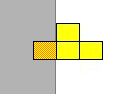
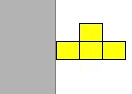
As shown in the tetromino map above, I have specified the pieces with a central axis (0, 0). The yellow 'T' shaped tetrominos is shown below in the downward and right-hand rotations (left and right respectively). With the downward rotation, part of the piece exists to the left of the central axis, at x=-1. Thus, the leftmost position that this item can be rendered with all parts visible is at x=1. It also has a part that is at x=1 and therefore the rightmost position it can be rendered is at x=8 (remember there are 10 horizontal positions numbered 0 to 9).
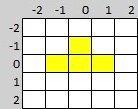
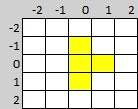
The right-hand rotation has no elements at x=-1 and therefore can be rendered at the x=0 position. Like the downward rotated piece, there is a part at x=1 and thus it's rightmost position is equal to x=8.
Two functions, leftMostPos() and rightMostPos() return the left- and right- most positions each tetromino can be rendered at and still have them completely visible on the screen.
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 |
int leftMostPos(byte type, byte rotation) {
switch (type) {
case SHAPE_SQ_RED:
return 0;
case SHAPE_T_YELLOW:
switch (rotation) {
case UP:
case DOWN:
case LEFT:
return 1;
case RIGHT:
return 0;
}
break;
case SHAPE_Z_GREEN: ...
case SHAPE_Z_BLUE: ...
case SHAPE_L_PURPLE: ...
case SHAPE_L_BLUE: ...
case SHAPE_I_ORANGE: ...
}
}
int rightMostPos(byte type, byte rotation) {
switch (type) {
case SHAPE_SQ_RED:
return BOARD_X_RIGHT_COL - 1;
case SHAPE_T_YELLOW:
switch (rotation) {
case UP:
case DOWN:
case RIGHT:
return BOARD_X_RIGHT_COL - 1;
case LEFT:
return BOARD_X_RIGHT_COL;
}
break;
case SHAPE_Z_GREEN: ...
case SHAPE_Z_BLUE: ...
case SHAPE_L_PURPLE: ...
case SHAPE_L_BLUE: ...
case SHAPE_I_ORANGE: ...
}
}
|
The canRotate() function accepts the tetromino's type, new rotation and current position as parameters. If the piece is too far left or too far right to support the rotation, it is moved into the board before a test is made to see if the board spaces / array elements are blank.
001 002 003 004 005 006 007 008 009 010 011 012 013 |
boolean canRotate(byte type, byte rotation, int x, int y) {
if (leftMostPos(type, rotation) > x) {
x = leftMostPos(type, rotation);
}
if (rightMostPos(type, rotation) < x) {
x = rightMostPos(type, rotation);
}
return canOccupySpace(type, rotation, x, y);
}
|
Updating the Board
The board array keeps track of stationery pieces - the one in motion is tracked using using two global variables, pieceX and pieceY. Once a piece can travel no further, the board array is update using the method updateBoard(byte type, byte rotation, int x, int y). As you can see from the parameters the tetromino type, rotation and position are passed into the method to determine which array elements to update.
Control is handled by an outer switch (line 003) which is conditioned on the type parameter. For each tetromino type, an inner switch conditioned on the rotation controls the actual updating. As the red square is symmetrical both laterally and longitudinally, their is no inner switch (lines 005 - 010). The yellow 'T' tetromino is not symmetrical either laterally and longitudinally and hence has a rotation switch with all four cases defined. The green 'Z' tetromino updates the same elements in the array whether when it is facing upwards or downwards - likewise when it is facing left or right.
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 |
void updateBoard(byte type, byte rotation, int x, int y) {
switch (type) {
case SHAPE_SQ_RED:
board[x][y] = pieceType;
board[x+1][y] = pieceType;
board[x][y+1] = pieceType;
board[x+1][y+1] = pieceType;
break;
case SHAPE_T_YELLOW:
switch (rotation) {
case UP:
board[x-1][y] = pieceType;
board[x][y] = pieceType;
board[x+1][y] = pieceType;
board[x][y+1] = pieceType;
break;
case LEFT:
if (y > 0) board[x][y-1] = pieceType;
board[x-1][y] = pieceType;
board[x][y] = pieceType;
board[x][y+1] = pieceType;
break;
case DOWN:
if (y > 0) board[x][y-1] = pieceType;
board[x-1][y] = pieceType;
board[x][y] = pieceType;
board[x+1][y] = pieceType;
break;
case RIGHT:
if (y > 0) board[x][y-1] = pieceType;
board[x][y] = pieceType;
board[x+1][y] = pieceType;
board[x][y+1] = pieceType;
break;
}
break;
case SHAPE_Z_GREEN:
switch (rotation) {
case UP:
case DOWN:
board[x-1][y] = pieceType;
board[x][y] = pieceType;
board[x][y+1] = pieceType;
board[x+1][y+1] = pieceType;
break;
case LEFT:
case RIGHT:
if (y > 0) board[x+1][y-1] = pieceType;
board[x][y] = pieceType;
board[x+1][y] = pieceType;
board[x][y+1] = pieceType;
break;
}
break;
case SHAPE_Z_BLUE: ...
case SHAPE_L_PURPLE: ...
case SHAPE_L_BLUE: ...
case SHAPE_I_ORANGE: ...
}
}
|
Wiring Diagram
The diagram below show the wiring diagram when using a standard Arduino Uno (or compatible) and the SmartGPU2. Click on the images to see a detailed drawing.


Downloads
Feel free to download, modify and adapt this code to your needs. Please credit me if you use some or all of this code in your own project. If you alter the code to fix bugs or add functionality, please submit them back to me and I will add them to the download.
 |
Arduino Source Code |



